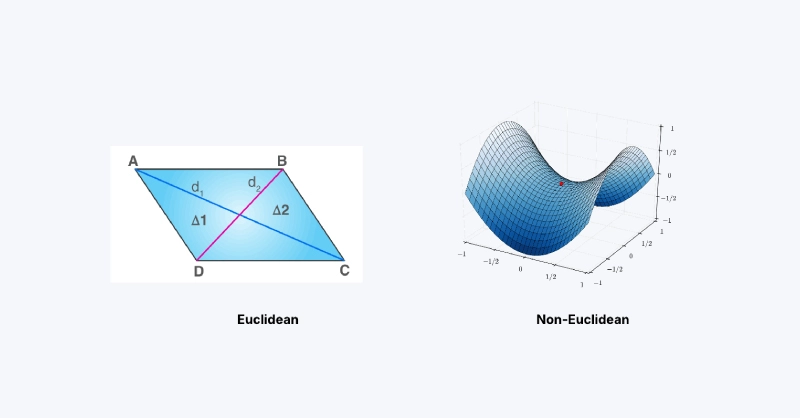
Geometric Deep Learning: AI Beyond Text & Images

Introduction

While traditional deep learning techniques have excelled at handling structured data like images and text, they often struggle when faced with irregular, complex data like molecules and networks of data. Geometric Deep Learning (GDL) is a machine learning methodology suitable for solving problems with irregular and complex data.

What is Geometric Deep Learning?

Geometric deep learning extends traditional deep learning approaches to handle non-Euclidean data, data that doesn't fit into regular grid-like or fixed structures like images or text. Geometric deep learning focuses on understanding relationships between data points, regardless of their spatial arrangement. This makes it particularly powerful for analyzing complex structures like molecular compounds, social networks, and meshes, where the connections between elements matter more than their specific locations.

While traditional deep learning architectures like convolutional neural networks (CNNs) and multilayer perceptrons (MLPs) excel at processing structured data formats such as image pixels arranged in grids, they face significant limitations when handling more complex data structures like non-Euclidean data. Workloads such as computer-aided drug discovery, medical 3D imaging, and social network fraud require a more sophisticated Graph Deep Learning approach.

Why Do Traditional Deep Learning Methods Struggle with Non-Euclidean Data?

Data that cannot be organized in a grid-like structure is non-Euclidean, meaning it doesn’t follow the standard rules of geometry. In non-Euclidean data, the distance between two points is not defined by a straight line, and instead is organized as graphs, meshes, or point clouds. Traditional deep learning methods are ineffective when dealing with irregular structures. Standard deep learning techniques assume that data is arranged in a regular, grid-like structure. When applied to non-Euclidean data:

• Local neighborhood patterns are not uniform: Unlike images, where every pixel has a fixed surrounding, nodes in a graph can have vastly different numbers and arrangements of neighbors.
• Invariances are different: For example, the concept of translation (moving an image slightly) works well with CNNs. However, graphs have invariances related to node ordering or connectivity that require different approaches.
• Loss of relational detail: Flattening irregular data to fit a grid often leads to the loss of the natural relationships inherent in the data.

Geometric Deep Learning Solves Weird and Complex Data

Geometric Deep Learning is the solution that extends deep learning techniques to handle non-Euclidean data, enabling AI models and algorithms to see relationships beyond proximity. By leveraging concepts like graph neural networks (GNNs) and message passing, the AI model can process data based on the relationships between interconnected nodes, a game-changer for applications where relationships are more important than absolute positions.

Instead of relying on grids, GDL focuses on the relationships between connected nodes. For example, in a molecular structure, each atom is a node, and bonds between them are the connections. A GDL model processes these relationships by:

• Graph Neural Networks (GNNs): These networks learn to aggregate information from a node’s neighbors through a process known as message passing.
• Message Passing: Each node gathers “messages” or information from its neighboring nodes and updates its state based on this combined data.
• Symmetry-Based Learning: GDL leverages inherent symmetries (such as permutation invariance in graphs) to ensure that the network’s output remains consistent regardless of the order in which nodes are processed.

Graph computations gather information from their neighbors, working in parallel. Where many calculations can happen at the same time, GPUs are the accelerator of choice. This makes the processing much faster and more efficient, especially for analyzing large networks like financial transactions or molecular structures.

Real-World Applications of Geometric Deep Learning

Geometric deep learning offers powerful capabilities for complex data analysis across various industries. By processing non-Euclidean data structures effectively, GDL enables valuable applications from biomolecular research to detection analysis. Here's how this technology creates opportunities across different sectors and addresses complex problems.

• Molecular Property Prediction: One of the most exciting applications of GDL is in the field of drug discovery:
  • Molecular Graphs: In chemistry, molecules are naturally represented as graphs where atoms are nodes and chemical bonds are edges.
  • Predicting Chemical Properties: GDL models can analyze these molecular graphs to predict important properties such as reactivity, toxicity, and binding affinity.
  • Accelerated Drug Discovery: With GDL, researchers can quickly screen vast libraries of compounds to identify promising drug candidates.
• 3D Modeling and Computer Vision: Geometric deep learning is also making waves in fields that require 3D data analysis:
  • Autonomous Driving: Self-driving cars rely on 3D sensors (like LiDAR) to capture point clouds that represent their surroundings. GDL can enhance scene understanding by processing these point clouds, enabling safer navigation.
  • Medical Imaging: In radiology, 3D models of organs are used to detect abnormalities. GDL helps in segmenting and analyzing these complex 3D structures.
  • Augmented Reality (AR): For AR applications, understanding the 3D layout of an environment is crucial. GDL improves the accuracy of depth estimation and object recognition in real time.
• Fraud Detection and Social Network Analysis: Another significant application of GDL is in detecting fraud and analyzing social networks:
  • Complex Networks: Fraud detection systems often deal with intricate transaction networks where fraudulent activities manifest as unusual patterns or connections.
  • Anomaly Detection: GDL models are excellent at identifying these anomalies by analyzing the structure of financial transaction graphs.
  • Social Media Analysis: In social networks, GDL can detect fake accounts or coordinated misinformation campaigns by finding irregular patterns in user interactions.

Key Takeaways

Geometric Deep Learning (GDL) provides powerful tools for handling non-Euclidean data structures, offering new approaches for data extraction, analysis, and evaluation. This capability opens up possibilities in areas where traditional deep learning methods face limitations.

Like most AI workloads, GPUs will continue to accelerate training by processing vast amounts of data in parallel and crucial for handling large-scale computations in real-time applications and large datasets.

• Scalability: Finding efficient ways to scale models across different hardware configurations remains an important focus area.
• Interpretability: Improving our understanding of GDL model decisions will be crucial for applications in healthcare and finance.
• Integration: Combining GDL with other AI methods (such as natural language processing or reinforcement learning) offers opportunities for more comprehensive solutions.

Its impact is already evident in fields like drug discovery, autonomous driving, medical imaging, and fraud detection. With continuous research and hardware improvements, Geometric Deep Learning can be applied in new ways with high potential for integrating with robotics, physics simulations, finance, and beyond.